
When you start your programming adventure, one of the most fundamental concepts that you encounter early on is the array. If you’ve recently switched to Python from another programming language, then you might be surprised that arrays are nowhere to be found as a built-in syntactical construct in Python. Instead of arrays, you typically use lists, which are slightly different and more flexible than classic arrays.
That said, Python ships with the lesser-known array module in its standard library, providing a specialized sequence type that can help you process binary data. Because it’s not as widely used or well documented as other sequences, there are many misconceptions surrounding the use of the array module. After reading this tutorial, you’ll have a clear idea of when to use Python’s array module and the corresponding data type that it provides.
In this tutorial, you’ll learn how to:
Before you dive in, you may want to brush up on your knowledge of manipulating Python sequences like lists and tuples, defining custom classes and data classes, and working with files. Ideally, you should be familiar with bitwise operators and be able to handle binary data in Python.
You can download the complete source code and other resources mentioned in this tutorial by clicking the link below:
Get Your Code: Click here to download the free source code that shows you how to use Python’s array with your numeric data.
Some developers treat arrays and Python’s lists as synonymous. Others argue that Python doesn’t have traditional arrays, as seen in languages like C, C++, or Java. In this brief section, you’ll try to answer whether Python has arrays.
To understand arrays better, it helps to zoom out a bit and look at them through the lens of theory. This will clarify some baseline terminology, including:
Computer science models collections of data as abstract data types (ADTs) that support certain operations like insertion or deletion of elements. These operations must satisfy additional constraints that describe the abstract data type’s unique behaviors.
The word abstract in this context means these data types leave the implementation details up to you, only defining the expected semantics or the set of available operations that an ADT must support. As a result, you can often represent one abstract data type using a few alternative data structures, which are concrete implementations of the same conceptual approach to organizing data.
Programming languages usually provide a few data structures in the form of built-in data types as a convenience so that you don’t have to implement them yourself. This means you can focus on solving more abstract problems instead of starting from scratch every time. For example, the Python dict data type is a hash table data structure that implements the dictionary abstract data type.
To reiterate the meaning of these terms, abstract data types define the desired semantics, data structures implement them, and data types represent data structures in programming languages as built-in syntactic constructs.
Some of the most common examples of abstract data types include these:
In some cases, you can build more specific kinds of abstract data types on top of existing ADTs by incorporating additional constraints. For instance, you can build a stack by modifying the queue or the other way around.
As you can see, the list of ADTs doesn’t include arrays. That’s because the array is a specific data structure representing the list abstract data type. The list ADT dictates what operations the array must support and which behaviors it should exhibit. If you’ve worked with the Python list , then you should already have a pretty good idea of what the list in computer science is all about.
Note: Don’t confuse the list abstract data type in computer science with the list data type in Python, which represents the former. Similarly, it’s easy to mistake the theoretical array data structure for a specific array data type, which many programming languages provide as a convenient primitive type built into their syntax.
The list abstract data type is a linear collection of values forming an ordered sequence of elements. These elements follow a specific arrangement, meaning that each element has a position relative to the others, identified by a numeric index that usually starts at zero. The list has a variable but finite length. It may or may not contain values of different types, as well as duplicates.
The interface of the list abstract data type resembles Python’s list , typically including the following operations:
| List ADT | Python’s list |
|---|---|
| Get an element by an index | fruits[0] |
| Set an element at a given index | fruits[0] = "banana" |
| Insert an element at a given index | fruits.insert(0, "banana") |
| Delete an element by an index | fruits.pop(0) , del fruits[0] |
| Delete an element by a value | fruits.remove("banana") |
| Delete all elements | fruits.clear() |
| Find the index of a given element | fruits.index("banana") |
| Append an element at the right end | fruits.append("banana") |
| Merge with another list | fruits.extend(veggies) , fruits + veggies |
| Sort elements | fruits.sort() |
| Get the number of elements | len(fruits) |
| Iterate over the elements | iter(fruits) |
| Check if an element is present | "banana" in fruits |
Now that you understand where the array data structure fits into the bigger picture, it’s time to take a closer look at it.
To visualize the traditional array data structure graphically, imagine a series of identically sized rectangular boxes lined up side by side, each holding a distinct value of a common type. For example, here’s what an array of integers could look like:

This array has seven elements, indexed from zero to six, all of which are integer numbers. Note that some of these values occur more than once.
At first glance, this looks just like the standard list in Python. After all, both represent the list abstract data type covered earlier. What makes the array data structure special is a few unique features. In particular, an array must be:
The first two traits make the array a random-access data structure, letting you instantly retrieve an element at any given index without having to traverse the whole array. When you know the memory address of the first element in the array, you can calculate the address of the desired element by applying a straightforward math formula:

To find the memory address Ai of an element located at index i in the array, you can take the address of your array, which is the same as the address of the first element A0 at index zero, and then add an offset. Because all elements have equal sizes, you can obtain the memory address offset by multiplying the target index i by the single element’s size in bytes.
This formula works as long as all elements have an identical size and appear next to each other. The downside of such a memory layout is the array’s fixed size, which becomes apparent once you wish to append, insert, or remove elements. However, you can only simulate resizing by making another array, copying existing elements to it, and disregarding your old array.
As a result, you end up frequently asking the operating system for an ever larger block of memory, and you waste time moving data from one place to another. It’s what makes insertions and deletions so inefficient with pure arrays.
One way to mitigate this limitation is to build an abstraction on top of your array that eagerly allocates more memory than necessary and keeps track of the current number of elements against the array’s capacity. When the underlying array becomes full, you can reallocate and copy the data to a larger array. That’s roughly what the Python list does under the surface to cope with dynamic resizing for you.
What about elements of the same type but variable sizes, such as strings?
Strings can have several representations in the computer memory. For example, the length-prefixed representation allocates an extra byte to encode the number of characters that follow. Another popular representation is the null-terminated string, which is essentially an array of bytes terminated by a special sentinel value called the null character. With such a representation, you can create an array of pointers to strings:
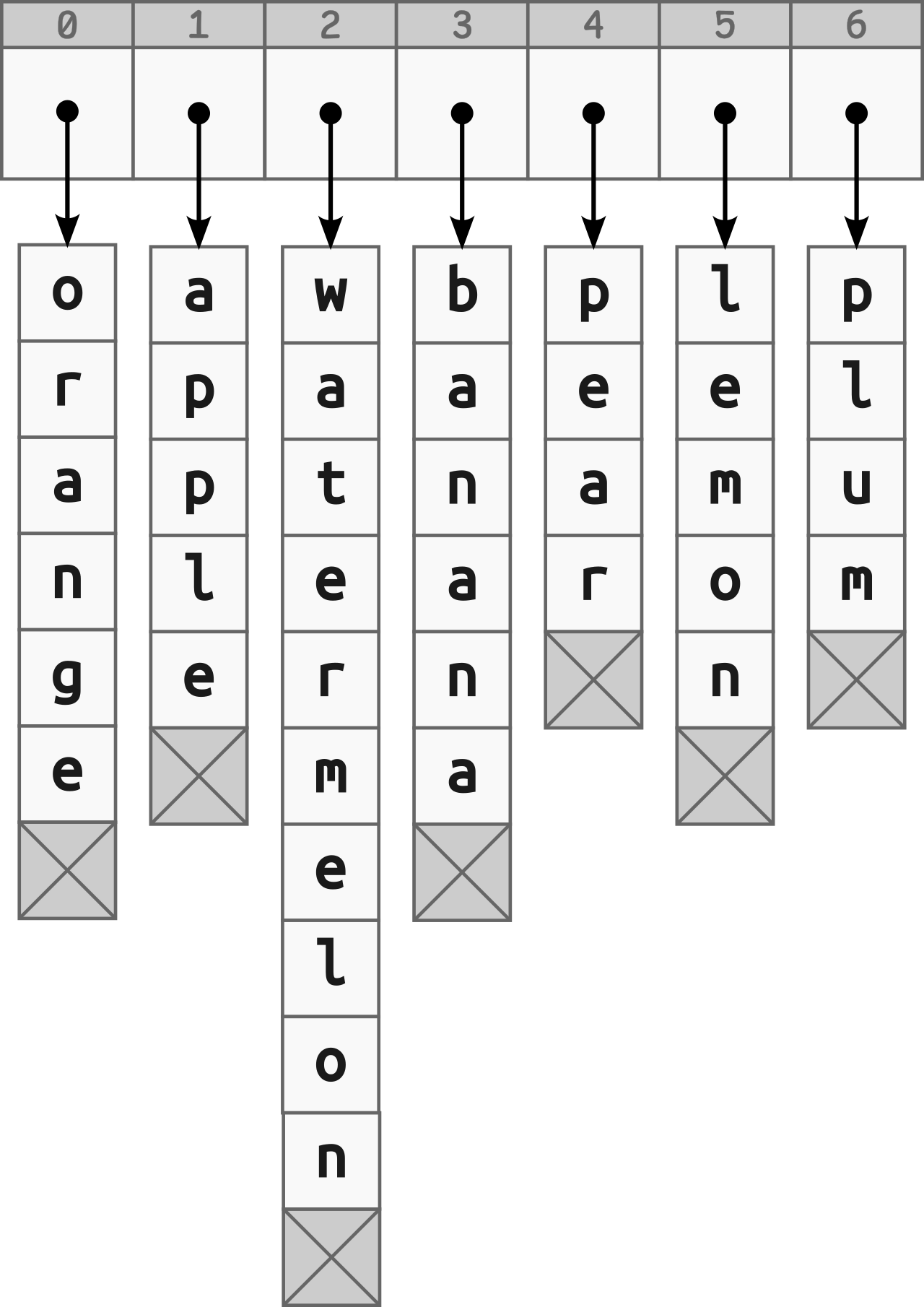
The array depicted above consists of pointers, or numeric addresses, each indicating a specific memory area where the given string begins. Even though the individual elements can have variable sizes and be scattered all over your computer’s memory, their corresponding pointers are plain integers of uniform size that fit into an array.
As it turns out, the array data structure isn’t the only way to implement the list abstract data type. Next up, you’ll learn about a popular alternative—the linked list.
At this point, you know that a list in computer science is an abstract data type and an array is one of its specific implementations. But why would you want to have more than one implementation, and how do you know which one to use?
The choice of a given data structure is vital for performance and memory efficiency. Most data structures offer a trade-off between the two, and they usually provide better time-space complexity for certain operations at the expense of others. Therefore, you should always pick a suitable data structure based on the requirements of the specific problem that you’re trying to solve.
For example, you can implement the list abstract data type using either an array or a linked list. Both are sequences of elements, but arrays will be more suitable in scenarios involving frequent lookups, while linked lists will work better when you anticipate a greater number of insertions or deletions.
Arrays always offer instant access to arbitrary elements but require extra time to add a new element. Conversely, linked lists allow for quick insertions but may take longer to find an element by index. That trade-off is the result of how both data structures organize data in memory.
If you’re interested in how the linked list achieves efficient insertions and deletions, then check out the relevant section of the corresponding article on Wikipedia to learn more. Now, the time has finally come to reveal whether Python has arrays or not.
Although a Python list represents the list abstract data type, its implementation isn’t the typical array or linked list. When you look at the CPython source code, you’ll find that the underlying PyListObject is a dynamic array of pointers to objects, allowing Python’s list to combine the benefits of both data structures. It’s cleverly optimized, ensuring quick lookups as well as insertions under most circumstances.
Python takes the idea of keeping an array of pointers to character strings, which was outlined before, a step further. It does so by retaining extra information about the data type of a value being pointed to from an internal array.
This makes Python’s list capable of storing heterogeneous elements of arbitrary types. On the other hand, this and the over-allocation make the Python list less memory-efficient than the classic array that you’d typically find in lower-level programming languages like C.
To sum up, Python internally relies on the array data structure but doesn’t directly expose it to you. The closest you can get to an array in Python is with the standard library’s array or NumPy’s ndarray data types. However, neither one of them provides a true array, as they can only hold numeric values.
On the Real Python website, you’ll find tons of resources on NumPy if you’d like to learn more about that library. And up next, you’ll read about the array module.
According to the reference documentation, the array module in Python defines an efficient array data structure whose elements are restricted to a handful of numeric types. Therefore, you won’t be able to use this module to create a generic array of arbitrary data types like strings or custom objects. What you can do with it, though, is compactly represent a large dataset for high-performance number crunching.
Admittedly, there are more powerful tools for numerical computing in Python, such as the previously mentioned NumPy library or pandas, among others. They’ll be a better fit for complex scientific computations and handling of multidimensional data in most cases. On the other hand, the array module ships with Python and is always available, so it’ll work best when you can’t or don’t want to install any third-party libraries.
Another common use case for the array module involves processing binary data that you might obtain from files or network sockets. It provides a convenient abstraction on top of raw bytes that would otherwise be difficult and inefficient to work with in pure Python. The module really shines in its relative simplicity and interoperability with C, which you’ll explore a bit later in this tutorial.
To whet your appetite, here’s what the basic syntax for creating an array in Python looks like:
array(typecode[, initializer]) After importing the array class from the array module, you must at least specify the type code for your array and optionally provide an initializer value. For example, this will create an array of four consecutive integers:
>>> from array import array >>> array("i", [1, 2, 3, 4]) array('i', [1, 2, 3, 4]) You’ll learn what this code does exactly and how to choose the type code in the following sections. Now, it’s time to get some practice with the array module in Python!
The first step before creating an instance of the array class from the array module is to decide on the common numeric type for its elements. Note that all array elements must have the same fixed numeric type. Once you choose from a few well-known numeric types, you can’t change your mind, so choose wisely. Because the numeric type determines the range of possible values, you won’t be able to store numbers outside that range in your array.
Unlike a Python list , which accepts arbitrary kinds of objects, a Python array can only accommodate numbers that fit a precise numeric type defined at the time of its creation. To use a real-life analogy, you can think of a Python list as a conveyor belt at a grocery store checkout counter. In contrast, a Python array is more like a carton specifically designed to hold eggs of a certain size and nothing else.
Python provides comparatively few numeric types through its syntax. They are:
Integers in Python have arbitrary precision, making them theoretically unbounded. Floating-point numbers and, by extension, complex numbers have a hard limit defined in the sys.float_info constant.
The Python standard library also ships with more specific types, including fractions and decimal numbers, which are built on top of the primitive types listed above. Beyond that, you’re on your own. While the numeric types available in Python cover the majority of high-level use cases, you might face some challenges when you start dealing with low-level binary data.
To address these challenges, the array module gives you much more granular control over the range of numbers. It exposes numeric types from the C programming language that are unavailable in standard Python. For example, you can use this module to declare an array of long integers or single-precision floats. Additionally, you can specify whether these numbers should be signed or unsigned, whereas all numbers in pure Python are always signed.
Note: When you access an array’s element, the interpreter takes care of wrapping the native data type into a high-level Python object that you can work with. This is known as boxing, while unboxing is the opposite operation.
There are thirteen numeric types in the array module, each represented by a single-letter type code, which you can reveal by accessing the typecodes variable:
>>> import array >>> array.typecodes 'bBuhHiIlLqQfd' Uppercase letters correspond to unsigned numbers, while lowercase letters represent signed ones. Their specific meanings are as follows:
| Type Code | C Type | Minimum Size in Bytes |
|---|---|---|
| b | signed char | 1 |
| B | unsigned char | 1 |
| h | signed short | 2 |
| H | unsigned short | 2 |
| i | signed int | 2 |
| I | unsigned int | 2 |
| l | signed long | 4 |
| L | unsigned long | 4 |
| q | signed long long | 8 |
| Q | unsigned long long | 8 |
| f | float | 4 |
| d | double | 8 |
| u | wchar_t | 2 |
As you can see, there are five pairs of integers consisting of the signed and unsigned flavor, two consistently signed floating-point types, and one wide character type that’s been deprecated since Python 3.3.
The more bytes you allocate, the greater the range of numbers you can represent. For example, a signed short requires two bytes or sixteen bits in memory, which gives you a range of numbers between -32,768 and 32,767. With its unsigned counterpart, you lose the ability to represent negative numbers, but you gain positive numbers up to 65,535. In other words, the range of representable values shifts upward.
Generally, knowing the number of bytes and whether the numeric type is signed lets you find the minimum and maximum values like so:
>>> def get_range(num_bytes, signed=True): . num_bits = num_bytes * 8 . if signed: . return -2 ** (num_bits - 1), 2 ** (num_bits - 1) - 1 . else: . return 0, (2 ** num_bits) - 1 . >>> get_range(num_bytes=2, signed=False) (0, 65535) >>> get_range(num_bytes=2, signed=True) (-32768, 32767) >>> get_range(num_bytes=4, signed=False) (0, 4294967295) >>> get_range(num_bytes=4, signed=True) (-2147483648, 2147483647) >>> get_range(num_bytes=8, signed=False) (0, 18446744073709551615) >>> get_range(num_bytes=8, signed=True) (-9223372036854775808, 9223372036854775807) The resulting tuples represent the minimum and maximum values included in each range of numbers.
Note that the table you saw earlier indicates the minimum number of bytes required to store a value of each data type. In practice, the actual number of bytes may be higher, depending on your system architecture and how the Python interpreter was compiled. For example, the int data type will occupy four bytes instead of just two on most modern computers:
>>> from array import array >>> array("i").itemsize 4 >>> array("i").typecode 'i' You can check a concrete array’s .itemsize attribute to find out exactly how many bytes one of its elements will consume in memory. Similarly, you can read the array’s .typecode attribute to show the letter that you used to create that array. Both attributes are read-only.
Note: The array class shares the name with its enclosing module, which can be confusing. In this tutorial, you’ll refer to the Python array as just array without using the fully qualified name, array.array . As long as you don’t need to import anything else apart from the class, you can use the from array import array statement to avoid prefixing the class name with the module name.
If you’re loading data from an external source into an array, then you should pick the type that exactly matches the corresponding format. Sometimes, it may not be possible to map a nonstandard numeric type onto one of the type codes in the array module. For example, OpenEXR files often use 16-bit floating-point numbers, while some WAV files encode data using 24-bit signed integers. Later, you’ll learn how to cope with such situations.
Otherwise, if you’re writing data of your own, then use the smallest type that can fit all possible values to optimize the memory use. Say you had an array of people’s ages ranging from 0 to 200. Because age can’t be negative, you may choose a type code corresponding to an unsigned byte, which can hold values from 0 to 255, giving you ample space.
By the way, if anyone you know lives to be older than two hundred years, then stop worrying about data types and ask them about their secret!
Once you determine which numeric type best suits your needs, you can finally create an array.
The array’s constructor expects only one required argument, which must specify the desired type of elements. When you omit the optional second argument, then you’ll define an empty array of numbers. For example, the following code creates an empty array of unsigned shorts, which are 2-byte integers without a sign:
>>> from array import array >>> empty = array("H") >>> len(empty) 0 Unlike the classic array data structure with a fixed length, Python’s array data type is dynamically sized. Therefore, you can add elements to an empty array later, and it’ll automatically resize itself accordingly.
Before learning how to populate an existing array with numbers, you’ll explore other ways of creating array instances in Python.
Instead of creating an empty array, you can alternatively populate your new array with elements from an initializer value passed as the second argument to the constructor. The initializer must be either a bytes instance or an iterable, provided that it consists of one of the following types:
Unlike some other programming languages, Python has no dedicated type for representing individual characters. An iterable of characters means a Python string or any other collection comprising strings of length one. Also, note that Python arrays don’t support complex numbers, even though they’re another numeric type in the language.
Below are a few examples demonstrating how you can use the Python array to interpret the same byte sequence in different ways. This lets you control how to read binary data from a file, for example. To test this out, generate sample bytes by encoding the snake emoji with UTF-8:
>>> snake_emoji = "\N ".encode("utf-8") >>> snake_emoji b'\xf0\x9f\x90\x8d' >>> len(snake_emoji) 4 >>> for byte in snake_emoji: . print(format(byte, "b")) . 11110000 10011111 10010000 10001101 The resulting byte sequence consists of four bytes, whose bits are depicted in the code block above. You can pass this byte sequence to a new array as the initializer value. Depending on the type code of the array, you’ll get wildly different results:
>>> array("b", snake_emoji) array('b', [-16, -97, -112, -115]) >>> array("B", snake_emoji) array('B', [240, 159, 144, 141]) >>> array("h", snake_emoji) array('h', [-24592, -29296]) >>> array("H", snake_emoji) array('H', [40944, 36240]) >>> array("i", snake_emoji) array('i', [-1919901712]) >>> array("I", snake_emoji) array('I', [2375065584]) >>> array("f", snake_emoji) array('f', [-8.913188736296437e-31]) When you declare an array of bytes using either the b or B type code, you get a new array of exactly four numbers corresponding to the individual byte values of your initializer. With wider types, such as the 2-byte short or the 4-byte integer and float, you get fewer elements in the array, but their magnitudes become larger.
Additionally, the arrays of signed types denoted with lowercase letter codes make Python interpret the numbers as negative. In this case, all four bytes of your initializer parameter have their most significant bit set to one, which becomes the sign bit.
If you already have another iterable container of integers, floats, or characters, then you can pass it to the array’s constructor to initialize the array with those values:
>>> array("i", [2 ** i for i in range(8)]) array('i', [1, 2, 4, 8, 16, 32, 64, 128]) >>> array("d", (1.4, 2.8, 4, 5.6)) array('d', [1.4, 2.8, 4.0, 5.6]) >>> array("u", "café") array('u', 'café') >>> array("u", ["c", "a", "f", "é"]) array('u', 'café') The first array contains eight integers, which are powers of two that you calculate in a list comprehension. The second array has four double-precision floating-point numbers derived from a tuple of numbers. The last two arrays represent the same characters obtained from a string and a list of individual single-character strings, respectively.
Internally, each Python array is a linear collection of numbers. The textual representation of a non-empty array depicts those numbers, except for the sequence of Unicode characters, which are rendered as a Python string instead. Nevertheless, characters are encoded as numerical code points under the hood, even though you don’t immediately see them.
You can initialize Python arrays in various ways depending on your needs. Moreover, you can clone an existing array, allowing you to work with a copy of the data without affecting your original array.
As a special case, you can provide another Python array as the initializer value to copy its elements. After all, an array is just an iterable of numbers that you can pass to the constructor:
>>> original = array("i", [1, 2, 3]) >>> cloned = array("i", original) >>> cloned == original True >>> cloned is original False First, you create an array of three integers, and then you feed it to a new array. The cloned array consists of the same values as the original prototype but exists as a separate entity in the memory. Both arrays compare as equal while being distinct objects, so you can modify them independently of each other.
Note: When you just want a copy of your array, you’re better off using the copy module, which the array supports through its memory-optimized special methods.
Note that both arrays contain elements of the same type. As long as the target array declares a superset type of the input array, or more generally, if your numbers can comfortably fit on the available range of values, then you can initialize the array:
>>> array("B", array("Q", range(256))) array('B', [0, 1, 2, (. ), 253, 254, 255]) Here, you initialize an array of unsigned bytes with another array whose elements use at least eight times more memory per number! However, because the actual values are small enough to fit on the target data type, there are no issues.
Something interesting happens when you feed an array of integers into a new array of floating-point numbers:
>>> array("f", array("i", [1, 2, 3])) array('f', [1.0, 2.0, 3.0]) The single- and double-precision floats are supersets of the input type, so Python automatically promotes your numbers to the broader type. As a side effect, you can freely mix integers and floats when initializing an array of floating-point numbers, as Python will eventually convert them to an appropriate representation:
>>> array("d", (1, 2.8, 4, 5.6)) array('d', [1.0, 2.8, 4.0, 5.6]) Your input tuple consists of Python integers and floats, all of which eventually get converted to the double-precision floating-point numbers.
However, this type conversion won’t work the other way around because it would result in a potential information loss about the fractional part of the floating-point numbers:
>>> array("i", array("f", [3.14, 2.72])) Traceback (most recent call last): . TypeError: 'float' object cannot be interpreted as an integer Trying to initialize an array of integers with floating-point numbers fails. There are many more things that can go wrong when you misuse the Python array, so you’ll next learn how to cope with them.
Remember that all elements that you stuff into an array, either through your initializer parameter or the interface that you’ll soon learn, must be compatible with the array’s declared type code. Otherwise, you’ll expose yourself to a host of problems.
First of all, when you supply an initializer containing a value of an unsupported data type, such as an iterable of complex numbers or Python strings instead of characters, then you’ll get a TypeError :
>>> array("d", [3 + 2j, 3 - 2j]) Traceback (most recent call last): . TypeError: must be real number, not complex >>> array("u", ["café", "tea"]) Traceback (most recent call last): . TypeError: array item must be unicode character In the first case, you declared an array of double-precision floating-point numbers but passed a list comprising complex numbers, which aren’t among the numeric types that arrays support. Then, you tried to initialize an array of Unicode characters using a list of multicharacter Python strings.
By the way, you can only provide an iterable of characters, such as a whole string or a list of its individual characters, when you use the "u" type code. For all other type codes, Python will raise a TypeError again:
>>> array("i", "café") Traceback (most recent call last): . TypeError: cannot use a str to initialize an array with typecode 'i' >>> array("i", ["c", "a", "f", "é"]) Traceback (most recent call last): . TypeError: 'str' object cannot be interpreted as an integer Arguably, the most common error is the integer overflow, which occurs when at least one of the numbers falls outside the supported range of values:
>>> array("B", [-273, 0, 100]) Traceback (most recent call last): . OverflowError: unsigned byte integer is less than minimum >>> array("b", [55, 89, 144]) Traceback (most recent call last): . OverflowError: signed char is greater than maximum The first call to the array’s constructor causes an underflow because unsigned bytes can’t be negative. Conversely, the second call results in an overflow, as the maximum value of a signed byte is 127.
A related problem might arise when you stumble on a number that exceeds the maximum value representable on the array’s data type:
>>> array("i", [10 ** 309]) Traceback (most recent call last): . OverflowError: Python int too large to convert to C long >>> array("Q", [10 ** 309]) Traceback (most recent call last): . OverflowError: int too big to convert >>> array("d", [10 ** 309]) Traceback (most recent call last): . OverflowError: int too large to convert to float >>> array("d", [1e309]) array('d', [inf]) In the first case, Python’s integer 10 309 exceeds the maximum value representable as a C long data type. In the second case, no corresponding C data type exists to accommodate such a huge number. Next, you try to initialize an array of floating-point numbers with a Python list containing your big integer.
Notice the difference between calculating an integer value with the exponentiation operator ( ** ) and specifying the corresponding floating-point literal, 1e309 , to represent the same value. Because floating-point numbers are bounded, Python automatically rounds the literal to a special value representing infinity. On the other hand, it raises the OverflowError during an attempt to convert an extremely large int to float .
At this point, you know that you can mix integers and floating-point numbers when initializing a Python array of an appropriate type. However, watch out for the loss of precision that may occur when you define an array of single-precision floats:
>>> array("f", (1.4, 2.8, 4, 5.6)) array('f', [1.399999976158142, 2.799999952316284, 4.0, 5.599999904632568]) With fewer bits at your disposal, you can’t represent some of these values exactly. Because of the floating-point representation error, they may get rounded to the nearest representable number.
Furthermore, when you move to multibyte numbers, then you must ensure that a byte sequence passed as the initializer value is a multiple of the given element size:
>>> array("H", b"\xff\x00\x80") Traceback (most recent call last): . ValueError: bytes length not a multiple of item size In this case, you tried initializing an array of unsigned shorts, which are two bytes long each, with a sequence of only three bytes. Because one byte is missing from your initializer, Python raises a ValueError with an appropriate message.
You’re now equipped with knowledge that will prevent you from falling into these common traps when you work with arrays in Python.
In this section, you’ll get some practice using arrays in Python. Along the way, you’ll learn that arrays resemble Python lists a lot, but at the same time, they have something special in store for you. You’ll learn how to make arrays work with other data types, and you’ll even access your array in a native C library!
Although the array class is fairly low level and used rather infrequently in Python, it’s a full-fledged sequence type alongside the more widespread list and tuple data types. As a result, you can use an array whenever a sequence or an iterable is expected. For example, you may pass an array of Fibonacci numbers to a relevant function:
>>> from array import array >>> fibonacci_numbers = array("I", [1, 1, 2, 3, 5, 8, 13, 21, 34, 55]) >>> len(fibonacci_numbers) 10 >>> sum(fibonacci_numbers) 143 The built-in len() function expects a sequence as an argument, whereas sum() takes an iterable of numbers, which an array certainly qualifies as. Thanks to Python’s duck typing, the exact data type doesn’t matter as long as the object at hand behaves as expected in the given context.
Naturally, being a finite sequence makes the array iterable. Therefore, you can loop over its elements or request the array to return an iterator object for manual traversal if you prefer:
>>> for i, number in enumerate(fibonacci_numbers): . print(f"[i>] = number:>2>") . [0] = 1 [1] = 1 [2] = 2 [3] = 3 [4] = 5 [5] = 8 [6] = 13 [7] = 21 [8] = 34 [9] = 55 >>> it = iter(fibonacci_numbers) >>> next(it) 1 In the example above, you first use the for loop along with the enumerate() function to visit each element of the Fibonacci sequence and then print the corresponding index and value. Next, you create a temporary iterator object and advance it once using the built-in next() function.
To a large extent, the interface of a Python array resembles a list , so it should make you feel right at home:
>>> fibonacci_numbers[-1] 55 >>> fibonacci_numbers[2:9:3] array('I', [2, 8, 34]) >>> fibonacci_numbers + array("I", [89, 144]) array('I', [1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144]) >>> 3 * array("I", [89, 144]) array('I', [89, 144, 89, 144, 89, 144]) >>> 42 in fibonacci_numbers False You can use the square bracket syntax for indexing and slicing an array, as well as the familiar operators, including the concatenation operator ( + ), repetition operator ( * ), and membership test operators ( in , not in ). Additionally, you’ll find most of Python’s list methods, such as .count() and .index() , in the array:
>>> fibonacci_numbers.count(1) 2 >>> fibonacci_numbers.index(13) 6 At the same time, high-level methods like .copy() , .clear() , and .sort() are missing from the array, but you can simulate them using alternative techniques.
Unlike the immutable tuples and strings, arrays in Python are unhashable and mutable sequences, meaning that you can modify their contents at will:
>>> fibonacci_numbers.append(89) >>> fibonacci_numbers.extend([233, 377]) >>> fibonacci_numbers.insert(-2, 144) >>> fibonacci_numbers.reverse() >>> fibonacci_numbers.remove(144) >>> fibonacci_numbers.pop(0) 377 >>> fibonacci_numbers.pop() 1 These methods modify your array in place, which explains why most of them don’t return any value. It means that you can change an existing array’s contents without creating a new array instance.
The subscription syntax lets you set or delete the value of the individual numbers at specified indices, as well as replace or remove entire array slices:
>>> fibonacci_numbers[0] = 144 >>> del fibonacci_numbers[-1] >>> fibonacci_numbers[2:9:3] = array("I", [3, 13, 55]) >>> del fibonacci_numbers[2:9:3] Note that you can only assign an array slice declared with an identical type code. In addition to this, be careful when you perform the extended slice assignment, which includes the third step parameter:
>>> fibonacci_numbers[2:9:3] = array("I", [3, 13, 55, 233]) Traceback (most recent call last): . ValueError: attempt to assign array of size 4 to extended slice of size 3 As with any sequence, you must ensure that the replacement slice has the same length as the one that you’re replacing when you use the extended syntax. That’s because the extra elements would produce gaps in your sequence, which must remain contiguous. On the other hand, regular slices with a step equal to one don’t have such a limitation.
Note: Check out Python’s Mutable vs Immutable Types to learn more about the differences between both kinds of data types.
Okay, you now know that an array shares an interface with other mutable sequence types in Python. Next up, you’ll learn about the unique features that set it apart.
Apart from the .itemsize and .typecode attributes that you saw earlier, a Python array provides additional methods that are specific to it. In particular, it has several methods for converting between arrays and other data types:
| To Array | From Array |
|---|---|
| .frombytes() | .tobytes() |
| .fromfile() | .tofile() |
| .fromlist() | .tolist() |
| .fromunicode() | .tounicode() |
The methods listed in the column on the left append elements to an array without overwriting any existing values. So, you can call them multiple times on the same instance to feed more numbers into your array. In fact, when you pass a list or a string as an initializer parameter to the array’s constructor, it’ll delegate the execution to some of these methods behind the curtain.
Conversely, the methods on the right allow you to represent the array’s content with the corresponding type. This may be useful when you want to process your data in pure Python or export it to a file.
The .fromfile() and .tofile() methods are the only ones that take a parameter, which must be a file object open in binary mode for reading or writing, respectively. The .fromfile() method also takes a mandatory second parameter with the number of elements to read. So, you must either know up front how many elements the file stores or retain this information separately:
>>> from array import array >>> from struct import pack, unpack >>> def save(filename, numbers): . with open(filename, mode="wb") as file: . file.write(numbers.typecode.encode("ascii")) . file.write(pack(", len(numbers))) . numbers.tofile(file) . >>> def load(filename): . with open(filename, mode="rb") as file: . typecode = file.read(1).decode("ascii") . (length,) = unpack(", file.read(4)) . numbers = array(typecode) . numbers.fromfile(file, length) . return numbers . >>> save("binary.data", array("H", [12, 42, 7, 15, 42, 38, 21])) >>> load("binary.data") array('H', [12, 42, 7, 15, 42, 38, 21]) In this code snippet, your custom save() function uses struct.pack() to encode the number of array elements in the file on a 4-byte unsigned integer ( I ). Note that struct uses format characters similar to the array’s type codes. Additionally, the function stores your array’s type code as an ASCII byte before dumping the actual array elements with .tofile() .
The load() function reverses these steps by first reading the type code and the number of elements in the file. It then creates an empty array of the correct numeric type, calls .fromfile() to populate it with the corresponding numbers from the file, and returns the filled array.
Note: Check out the maze solver project for a hands-on example of using array and struct to handle a custom binary file format.
When you share binary files between operating systems or computer architectures, you must consider the potential differences in their endianness or byte ordering. There are two major types of endianness:
If you don’t take extra steps to handle these differences, then you’ll face issues when transferring binary data between two systems that use different byte order. More specifically, you’ll misinterpret and corrupt your data by reading the individual bytes in the wrong order. So, when one system writes a number like 42, it may appear as 704,643,072 on the other end:
>>> unpack(", pack(", 42)) # Consistent byte order (42,) >>> unpack(">I", pack(", 42)) # Inconsistent byte order (704643072,) While the struct module gives you control over the byte order and alignment through the angle bracket syntax ( < and >), Python arrays remain agnostic about the interpretation of their underlying bytes. However, they do let you swap the byte order within each array element if you know that it requires adjustment:
>>> data = b"\x00\x00\x00\x00\x00\x00\x00\x01\x00\x00\x00\x00\x00\x00\x00\x02" >>> data_points = array("L", data) >>> data_points array('L', [72057594037927936, 144115188075855872]) >>> data_points.byteswap() >>> data_points array('L', [1, 2]) If you read raw data from a file into a Python array knowing that the file format uses a different byte order than your system, then you can bring it to the correct endianness by reversing the bytes. Note that .byteswap() has no effect on arrays of single bytes ( b and B ) because the order only applies to multibyte numbers, such as short or long integers.
You’ve already delved deep into the complexities of binary data handling in Python with the help of arrays. Still, you can go even deeper by engaging a custom C library for processing your array elements, which you’ll explore next.
Last but not least, the Python array supports the buffer protocol, making it a bytes-like object that you can use in contexts requiring direct access to the low-level memory region in CPython. This lets you integrate with C and C++ libraries seamlessly while avoiding unnecessary data copying.
To get the details about the underlying buffer, call your array’s .buffer_info() method:
>>> from array import array >>> data_points = array("L", [72057594037927936, 144115188075855872]) >>> data_points.buffer_info() (140039807835648, 2) >>> id(data_points) 140039810496960 It returns a tuple comprising the memory address of the buffer and the total number of elements that it currently holds. Notice that the memory address of the buffer is slightly different than the address of the Python array object that wraps it.
You can calculate the total number of bytes allocated for the array’s buffer by using the following code:
>>> data_points.itemsize * data_points.buffer_info()[1] 16 Because there are two elements in the data_points array and each element is eight bytes long, the total size amounts to sixteen bytes. You may need this information when accessing the buffer from a C extension module.
Writing a Python extension module in C or another compiled programming language is tedious. Fortunately, there’s a more straightforward way, which involves the standard-library ctypes module. It allows for calling native functions from a shared library loaded dynamically into your Python script. Because arrays in Python implement the buffer protocol, you can obtain a pointer to the corresponding memory region.
Remember that you can download the supporting materials by clicking the link below, which may help if you get stuck or don’t want to type the code by hand:
Get Your Code: Click here to download the free source code that shows you how to use Python’s array with your numeric data.
First, define a bare-bones function in C that’ll take an array of numbers and modify its elements in place by incrementing them:
C cruncher.cvoid increment(int* numbers, unsigned int length) for (int i = 0; i length; i++) numbers[i]++; > > The function expects a pointer to an array of signed integers as well as the length of the array. The second argument is necessary because C doesn’t keep track of the number of elements in arrays. Then, the function loops over array indices and increments each element by one.
If you’re on a Linux distribution and have the GNU C compiler installed, then you can issue the following command to turn this code into a shared library:
$ gcc -shared -fPIC -O3 -o cruncher.so cruncher.c The -fPIC flag makes the compiler generate position-independent code, which is required for loading a dynamic-link library into another process, whereas -O3 enables optimizations.
You can now return to Python, load the compiled library, and call your custom C function against a non-empty Python array:
>>> from array import array >>> from ctypes import POINTER, c_int, c_uint, cdll >>> cruncher = cdll.LoadLibrary("./cruncher.so") >>> cruncher.increment.argtypes = (POINTER(c_int), c_uint) >>> cruncher.increment.restype = None >>> python_array = array("i", [-21, 13, -8, 5, -3, 2, -1, 1, 0, 1]) >>> c_array = (c_int * len(python_array)).from_buffer(python_array) >>> cruncher.increment(c_array, len(c_array)) >>> python_array array('i', [-20, 14, -7, 6, -2, 3, 0, 2, 1, 2]) You start by specifying the native function’s signature, which consists of the argument types and the return value type. In this case, your function takes a pointer to signed integers and an unsigned integer without returning anything. It’s vital that you define this signature, or else Python won’t be able to call the C function correctly.
Next, you create a Python array filled with a few positive and negative Fibonacci numbers using the "i" type code, which corresponds to the signed integer type in C. You then wrap your Python array in a lightweight adapter, which you later pass to the native increment() function.
What’s important, calling .from_buffer() on the array adapter doesn’t allocate new memory:
>>> id(memoryview(python_array)) 140664913614336 >>> id(memoryview(c_array)) 140664913614336 As you can see, the memory views of both the Python and C arrays have identical addresses, which proves that they point to the same buffer under the surface. In other words, your C function directly operates on the Python array without needing to copy the data, significantly reducing memory use and improving performance.
If this wasn’t enough evidence that the C function indeed modifies your Python array, notice how its elements change after you call increment() . They all increase by one, which is exactly what the compiled function is supposed to do.
Combining Python with C through the buffer protocol can be incredibly efficient, especially for large numeric arrays, offering considerable performance gains over pure Python code. It’s one of the secrets behind NumPy arrays being as fast and efficient as they are.
Now, it’s time to determine precisely how much Python’s arrays outperform conventional lists.
To be fair, comparing arrays to other sequences in Python is a bit like comparing apples to oranges, as they have different uses. The closest equivalent of a Python array would be a list of numbers.
However, lists are general-purpose object containers that can deal with diverse data types, while arrays have a fixed type constrained to numbers. Moreover, lists are built into the syntax and offer plenty of conveniences. On the other hand, arrays are trickier to use but have little memory overhead and can leverage efficient low-level mechanisms.
Based on the knowledge that you’ve gained so far, you might expect Python arrays to be faster than lists in performing complex numerical computations. To put these expectations to the test, you’ll need to execute some benchmarks. In Python, it’s customary to use the standard timeit module to measure code performance:
>>> from array import array >>> from timeit import timeit >>> large_list = list(range(10**6)) >>> large_array = array("I", large_list) >>> timeit(lambda: sum(large_list), number=100) 0.8359777819969167 >>> timeit(lambda: sum(large_array), number=100) 2.718988453001657 First, you create a list of one million Python integers and an identical array of C unsigned integers. Then, you call timeit() against both sequences to measure how long it takes to sum their elements. You execute the specified code snippets one hundred times to account for system noise.
Note: System noise includes background processes of the operating system or other applications running on your machine. These processes aren’t directly related to your code but may affect its performance. By running the benchmark multiple times, you can average the results to get a more accurate representation of the actual performance of your code snippet.
Somewhat surprisingly, the standard Python list blows the array out of the water. The absolute number of elapsed seconds is irrelevant because it’ll vary depending on the sequence length, your computer’s speed, and other factors. However, the conclusion is that the same code runs a few times faster when it relies on the list rather than the array!
You can summarize the explanation of this unexpected outcome using two words: boxing overhead. In short, the built-in sum() function has to convert each array element from a native C representation to the corresponding Python wrapper, which adds significant overhead. Tim Peters gives a more detailed description of this phenomenon on Stack Overflow:
The storage is “unboxed,” but every time you access an element, Python has to “box” it (embed it in a regular Python object) in order to do anything with it. For example, your sum(A) iterates over the array and boxes each integer, one at a time, in a regular Python int object. That costs time. In your sum(L) , all the boxing was done at the time the list was created.
So, in the end, an array is generally slower but requires substantially less memory. (Source)
Fair enough. When you process your array in pure Python, you’ll most likely lose to other sequence types in terms of execution speed. It’s only when you can avoid the boxing overhead by accessing your array in a compiled C library directly that you stand a chance. What about the memory savings promised by Python arrays?
To check the size of a Python object in bytes, call sys.getsizeof() or use a third-party library like Pympler, which may give more accurate results. Extend your experiment from earlier by adding a step to measure how much memory your array and list of numbers consume:
>>> from sys import getsizeof >>> from pympler.asizeof import asizeof >>> getsizeof(large_array) 4000080 >>> asizeof(large_array) 4000080 >>> getsizeof(large_list) 8000056 >>> asizeof(large_list) 40000056 The Python standard library and Pympler agree on the size of the array. It seems to be correct because one million 32-bit integers is about four megabytes, or four million bytes. The extra eighty bytes correspond to the Python array’s metadata.
In contrast, the list comprising identical values is at least twice as large. Remember that a Python list maintains an array of pointers in addition to the actual elements. Therefore, you need one million integer numbers and another million integer pointers in this case, plus fifty-six bytes of metadata.
According to Pympler, the Python list uses as much as ten times more memory than the equivalent array. The third-party library recursively traverses a fragment of the object tree in memory, taking into account any other objects that might be referenced. Hence, it reports a larger size than sys.getsizeof() .
To conclude, Python arrays may be slower than lists, mainly due to the boxing overhead when you don’t take advantage of their buffer interface in C. However, arrays can significantly reduce the memory size of your data, which might tip the balance in their favor depending on your specific use case. Lastly, they can make integrating Python with low-level code easier.
The array module lets you declare an array of numbers using one of several low-level C types, while Python natively supports only three types of numbers. At first sight, this may seem like a lot. Still, those extra numeric types won’t be enough for you in some situations. This section will give you an idea of when and how to deal with nonstandard numeric types that you may find in the wild.
High-level programming languages provide convenient abstractions over the binary representations of numbers to let you focus on solving bigger problems. For example, Python has int , float , and complex , while JavaScript has only one Number type to rule them. Slightly lower-level languages like C and C++ come with a broader spectrum of numeric types to offer greater control over data storage, which is required for working with binary data.
Note: Contemporary JavaScript comes with a more specialized BigInt type to address the shortcomings of floating-point numbers, which became apparent once developers started using JavaScript on the back end. Although BigInt was introduced in the official ECMAScript specification in 2020, some JavaScript engines already supported it a few years earlier.
The IEEE 754 specification governs the representation and behavior of real numbers in most modern computers, regardless of the programming language. Whether you use a Python float , a JavaScript Number , or a C double , they should work the same. Note that in C and C++, among many other languages, you can choose between single-precision or double-precision floating-point numbers. With higher-level languages, you often only have the latter.
When storing integer numbers in memory, computers typically use the two’s complement representation, which can handle both positive and negative values. In some languages, you can decide whether to use signed or unsigned integers. With unsigned numbers, you can effectively double the representable range of values. Python’s integers are always signed but use clever internal representations to give them arbitrary precision at a small cost.
As a Python developer, you might’ve never thought of the intricacies of numeric types and their representations. However, once you read binary data from an external source, you must know how to correctly interpret the corresponding byte sequences. At the very least, you should know the answers to the following questions:
Due to the architectural design of modern computers, which are optimized for working with octets, as well as for historical reasons, standard numeric types have bit lengths that are powers of two. For example, common bit lengths include eight, sixteen, thirty-two, and sixty-four bits. Programming languages provide built-in data types that correspond to these bit lengths, such as char , short , int , and long in C.
The array module in Python exposes these numeric types so that you can use them in your arrays. Unfortunately, there’ll be times when the binary data that you need to work with doesn’t exactly match any of these standard numeric types. Therefore, you’ll need to find a work-around to process your data properly.
While 8-bit bytes and their multiples defined by powers of two are the standard units of digital information, not all data types follow this pattern. Legacy systems or specialized applications may employ nonstandard numeric types.
For instance, many music streaming services offer content in a format based on 24-bit signed integers per sample to strike a balance between good audio quality and the amount of data to transfer. By using a nonstandard audio bit depth, they achieve a noticeably higher quality than the standard 16-bit CDs but still maintain a reasonably small size.
Unfortunately, this creates a problem for you because Python arrays don’t provide a type code for 24-bit integers. You’ll need to allocate the next larger data type per audio sample in your array, which happens to be a 32-bit integer. Then, you’ll need to manually reinterpret the corresponding bytes, which you can do by calling int.from_bytes() on them :
>>> audio_sample = b"\x7f\xfc>" >>> int.from_bytes(audio_sample) 8387646 The audio sample in the example above consists of three bytes or twenty-four bits. After calling the int.from_bytes() class method, you convert raw bytes into a Python integer representing the relative amplitude of the sound wave that enters your speakers.
Check out the following code snippet, which combines this technique with a Python array:
>>> import wave >>> with wave.open("PCM_24_bit_signed.wav", mode="rb") as wave_file: . if wave_file.getsampwidth() == 3: . raw_bytes = wave_file.readframes(wave_file.getnframes()) . samples = array( . "i", . ( . int.from_bytes( . raw_bytes[i : i + 3], . byteorder="little", . signed=True, . ) . for i in range(0, len(raw_bytes), 3) . ), . ) . Using the Python wave module, you load stereo frames, each consisting of the left and right audio channels, from a 24-bit PCM-encoded WAV file. Next, you create a new array of 32-bit signed integers and initialize it using a generator expression that iterates over the raw bytes three elements at a time. For each slice, you interpret its bytes, explicitly setting the expected byte order and sign.
Note: The implementation above is suboptimal because it reads the entire file into memory. That’s intentional to keep the code simple. However, in practice, you’d want to read audio samples in chunks using a streaming approach to reduce memory use and increase efficiency.
To verify that you’ve loaded your audio samples correctly, you can do some math:
>>> len(raw_bytes) 40600914 >>> len(samples) 13533638 >>> wave_file.getnframes() 6766819 The raw bytes represent the content of the audio file. In this case, that amounts to just over forty megabytes, or 40,600,914 bytes of data. When you divide this number by the three bytes per sample, you get a total of 13,533,638 stereo samples, or 6,766,819 samples per channel, which is also the number of frames.
Because you declared your array with the "i" type code, which stands for 32-bit signed integers, the total amount of memory that it consumes surpasses the file’s original size:
>>> samples.itemsize 4 >>> samples.itemsize * len(samples) 54134552 Instead of roughly forty megabytes, your array clocks in at fifty-four, which is one-third more. That makes sense, as each array element uses four instead of three bytes.
Unfortunately, there’s no way to avoid this extra cost with nonstandard numeric types, even if you declare your array in the C programming language. Anyhow, you now know how to emulate these nonstandard numeric types using the available tools.
Congratulations! You’ve mastered the rare skill of using arrays in Python to efficiently represent numbers in the computer memory. You can now read binary data encoded on low-level numeric types that are missing from pure Python. Additionally, you know how to emulate exotic types in your arrays to work with online audio streams, for example.
Along the way, you’ve seen how arrays can help you tightly integrate Python code with compiled libraries loaded at runtime. In particular, you practiced accessing your Python array directly from the native code in C and processing its elements close to the metal. This not only ensured memory-efficient storage but also a significant performance boost.
In this tutorial, you’ve learned how to:
Have you been using arrays in Python before? If so, what problem did they help you solve? Share in the comments below!
Get Your Code: Click here to download the free source code that shows you how to use Python’s array with your numeric data.